Strength of Materials - Stress
|
2. Stresses
Stress is defined as the internal resistance
set up by a body when it is deformed. It is
measured in N/m2 and this unit is specifically
called Pascal (Pa). A bigger unit of stress
is the mega Pascal (MPa).
1 Pa = 1N/m2,
1MPa = 106 N/m2 =1N/mm2.
2.1. Three Basic
Types of Stresses
Basically three different types of stresses
can be identified. These are related to the
nature of the deforming force applied on the
body. That is, whether they are tensile, compressive
or shearing.
|
| |
|
|
|
| 2.1.1.
Tensile Stress
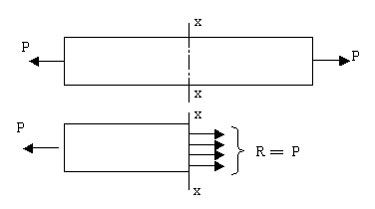
Consider a uniform bar of cross sectional area
A subjected to an axial tensile force P. The
stress at any section x-x normal to the line
of action of the tensile force P is specifically
called tensile stress pt . Since internal resistance
R at x-x is equal to the applied force P, we
have,
pt = (internal resistance at x-x)/(resisting
area at x-x)
=R/A
=P/A.
Under tensile stress the bar suffers stretching
or elongation.
|
| |
| |
|
| |
2.1.2. Compressive
Stress
If the bar is subjected to axial compression
instead of axial tension, the stress developed
at x-x is specifically called compressive stress
pc.
pc =R/A
= P/A.
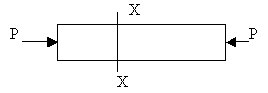
Under compressive stress the bar suffers shortening.
|
| |
2.1.3.
Shear Stress
Consider the section x-x of the rivet forming
joint between two plates subjected to a tensile
force P as shown in figure.
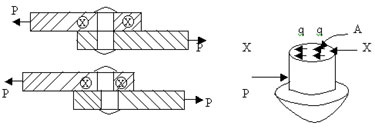
|
| |
The
stresses set up at the section x-x acts along
the surface of the section, that is, along a direction
tangential to the section. It is specifically
called shear or tangential stress at the section
and is denoted by q.
q =R/A
=P/A. |
| |
2.2.
Normal or Direct Stresses
When the stress acts at a section or normal
to the plane of the section, it is called a
normal stress or a direct stress. It is a term
used to mean both the tensile stress and the
compressive stress.
2.3. Simple and
Pure Stresses
The three basic types of stresses are tensile,
compressive and shear stresses. The stress developed
in a body is said to be simple tension, simple
compression and simple shear when the stress
induced in the body is (a) single and (b) uniform.
If the condition (a) alone is satisfied, the
stress is called pure tension or pure compression
or pure shear, as the case may be.
2.4. Volumetric
Stress
Three mutually perpendicular like direct stresses
of same intensity produced in a body constitute
a volumetric stress. For example consider a
body in the shape of a cube subjected equal
normal pushes on all its six faces. It is now
subjected to equal compressive stresses p in
all the three mutually perpendicular directions.
The body is now said to be subjected to a volumetric
compressive stress p.
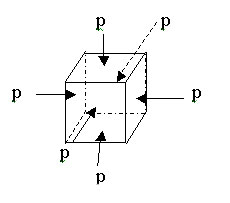
Volumetric stress
produces a change in volume of the body without
producing any distortion to the shape of the
body.
|
|